Como parte de su impulso para expandirse al mercado europeo, MacNeil Shellfish, con sede en Escocia, presentará nuevos productos cocidos...
Boeing dijo el miércoles que perdió 355 millones de dólares debido a menores ingresos en el primer trimestre, otra señal...
Rich Polk/NBC vía Getty Images Imágenes en vídeo de un accidente ocurrido en el set de una película de Eddie...
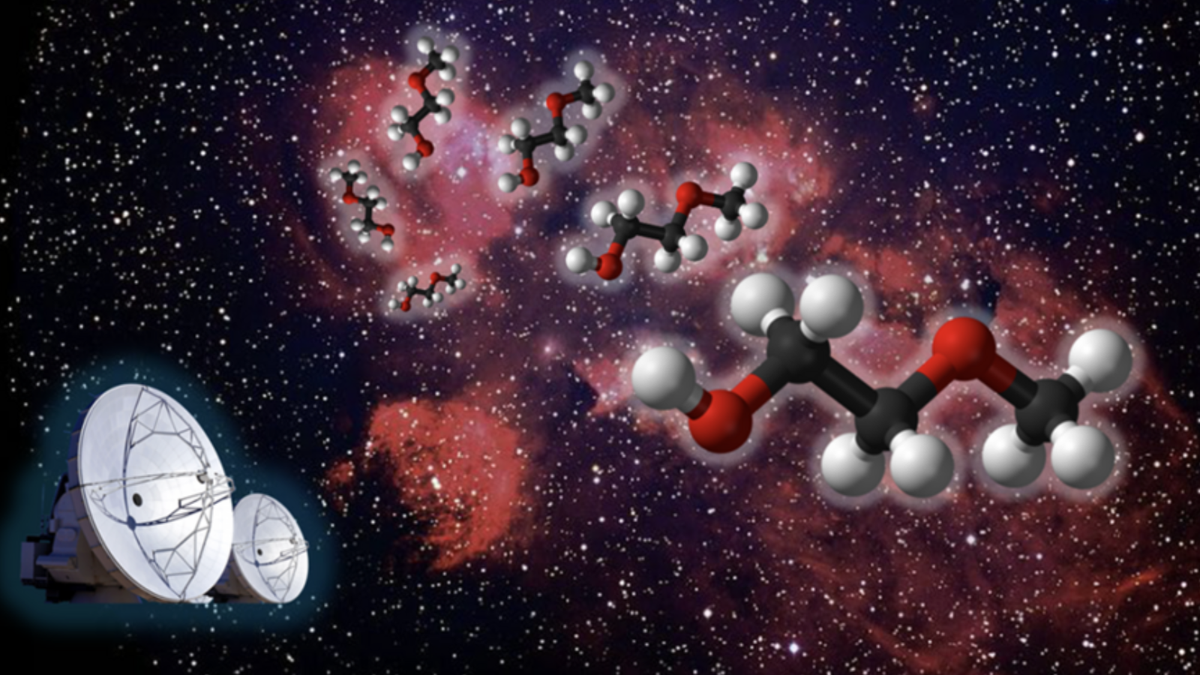
Los científicos han descubierto una partícula espacial hasta ahora desconocida mientras examinaban una región relativamente cercana al nacimiento de estrellas...
No habrá drama en la cima del draft el jueves por la noche.El mariscal de campo de la USC, Caleb...
Apple lanzó hoy varios modelos de lenguajes grandes (LLM) de código abierto que están diseñados para ejecutarse en dispositivos en...
Enlaces de ruta de navegaciónviajarPublicado el 24 de abril de 2024 • Última actualización hace 1 hora • leo por...
Ministerio de Transporte el miércoles Nuevas reglas anunciadas Nos enfocamos en dos de los problemas más difíciles y molestos en...
cnn — En la superficie, Baby Reindeer de Netflix tiene todo el encanto de un buen episodio de Dateline: está...
En 1964, los paleontólogos descubrieron el cráneo de un ancestro del salmón gigante en una cantera cerca de la ciudad...